Unity如何實(shí)現(xiàn)圖形相交檢測(cè)
小編這次要給大家分享的是Unity如何實(shí)現(xiàn)圖形相交檢測(cè),文章內(nèi)容豐富,感興趣的小伙伴可以來(lái)了解一下,希望大家閱讀完這篇文章之后能夠有所收獲。
成都創(chuàng)新互聯(lián)公司專注于正安企業(yè)網(wǎng)站建設(shè),成都響應(yīng)式網(wǎng)站建設(shè)公司,商城網(wǎng)站制作。正安網(wǎng)站建設(shè)公司,為正安等地區(qū)提供建站服務(wù)。全流程定制制作,專業(yè)設(shè)計(jì),全程項(xiàng)目跟蹤,成都創(chuàng)新互聯(lián)公司專業(yè)和態(tài)度為您提供的服務(wù)
前言
圖形相交檢測(cè)常常用在傷害判定,使用自定義的圖形相交檢測(cè),可以在一定程度上控制性能。
比如2D格斗游戲中使用的矩形包圍盒(AABB),一些動(dòng)作游戲中常常出現(xiàn)的扇形攻擊。
2D的圖形相交檢測(cè)能夠滿足大部分的需求,且可以拓展成為柱狀的3D物體,2D比3D的計(jì)算復(fù)雜度會(huì)低很多,3D的圖形檢測(cè)原理與2D相似,本文會(huì)實(shí)現(xiàn)幾個(gè)圓形與其他2D圖形的相交檢測(cè):
1、圓形與圓形
2、圓形與膠囊體
3、圓形與扇形
4、圓形與凸多邊形
5、圓形與AABB
6、圓形與OBB
通過(guò)簡(jiǎn)單化處理,把被判定物都處理成由圓柱或多個(gè)圓柱構(gòu)成的區(qū)域,所以只需要考慮圓形與其他形狀的相交。
圓形與圓形
兩個(gè)圓形的相交檢測(cè)非常簡(jiǎn)單直觀,只需要判斷半徑只和與距離的大小。
定義圓形區(qū)間:
/// <summary>
/// 圓形區(qū)間
/// </summary>
public struct CircleArea
{
public Vector2 o;
public float r;
}o ——圓心坐標(biāo)
r ——圓半徑
相交判斷:
/// <summary>
/// 判斷圓形與圓形相交
/// </summary>
/// <param name="circleArea"></param>
/// <param name="target"></param>
/// <returns></returns>
public static bool Circle(CircleArea circleArea, CircleArea target)
{
return (circleArea.o - target.o).sqrMagnitude < (circleArea.r + target.r) * (circleArea.r + target.r);
}分離軸定理
分離軸定理(separating axis theorem, SAT)分離軸定理是指,兩個(gè)不相交的凸集必然存在一個(gè)分離軸,使兩個(gè)凸集在該軸上的投影是分離的。
判斷兩個(gè)形狀是否相交,實(shí)際上是判斷分離軸是否能把兩個(gè)形狀分離。若存在分離軸能使兩個(gè)圖形分離,則這兩個(gè)圖形是分離的。
基于以上理論,尋找分離軸是我們要做的工作,重新考慮兩個(gè)圓形的相交檢測(cè),實(shí)際上我們做的是把圓心連線的方向作為分離軸:
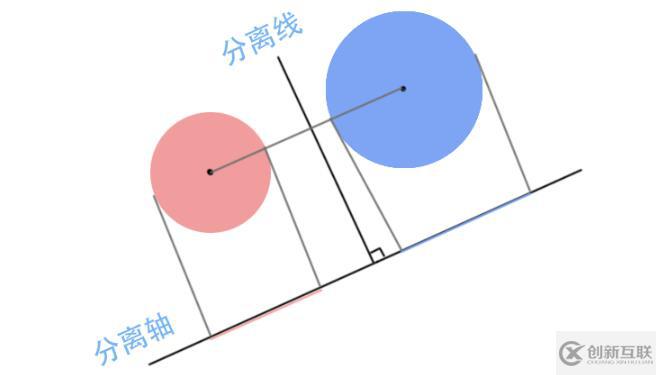
上圖中兩圖形的投影在分離軸上是分離的,存在分離線將兩者隔開(kāi),于是我們可以斷定兩圖形是分離的。
膠囊體的本質(zhì)
定義一個(gè)線段 u,距離 d。膠囊體實(shí)際上是與線段 u 的最短距離小于 d 的點(diǎn)的集合。判斷一個(gè)點(diǎn) x 處于膠囊體內(nèi)部,就是判斷點(diǎn)與線段的距離。
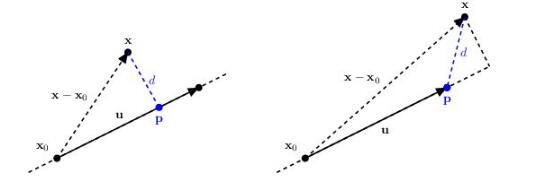
求點(diǎn) x 與線段 u 最短距離的過(guò)程是:
1、求出點(diǎn) x 在線段 u 所在直線上的投影點(diǎn) P;
2、將投影點(diǎn) P 限制在線段的范圍內(nèi)(如右圖中投影點(diǎn)不在線段內(nèi),則限定到線段內(nèi));
3、x 與 P 的距離即為所求;
/// <summary>
/// 線段與點(diǎn)的最短距離。
/// </summary>
/// <param name="x0">線段起點(diǎn)</param>
/// <param name="u">線段向量</param>
/// <param name="x">求解點(diǎn)</param>
/// <returns></returns>
public static float SqrDistanceBetweenSegmentAndPoint(Vector2 x0, Vector2 u, Vector2 x)
{
float t = Vector2.Dot(x - x0, u) / u.sqrMagnitude;
return (x - (x0 + Mathf.Clamp01(t) * u)).sqrMagnitude;
}為避免開(kāi)方計(jì)算,結(jié)果使用距離的平方。
圓形與膠囊體
分離軸是線段上距離圓心最近的點(diǎn)P與圓心所在方向。
定義膠囊體:
/// <summary>
/// 膠囊體
/// </summary>
public struct CapsuleArea
{
public Vector2 X0;
public Vector2 U;
public float d;
}相交判斷:
/// <summary>
/// 判斷膠囊體與圓形相交
/// </summary>
/// <param name="capsuleArea"></param>
/// <param name="circleArea"></param>
/// <returns></returns>
public static bool Capsule(CapsuleArea capsuleArea, CircleArea circleArea)
{
float sqrD = SegmentPointSqrDistance(capsuleArea.X0, capsuleArea.U, circleArea.o);
return sqrD < (circleArea.r + capsuleArea.d) * (circleArea.r + capsuleArea.d);
}圓形與扇形
當(dāng)扇形角度大于180度時(shí),就不再是凸多邊形了,不能適用于分離軸理論。我們可以找出相交時(shí)圓心的所有可能區(qū)域,并把區(qū)域劃分成可以簡(jiǎn)單驗(yàn)證的幾個(gè)區(qū)域,逐個(gè)試驗(yàn)。
這里共劃分了2個(gè)區(qū)間
1、半徑為兩者半徑和的扇形區(qū)間,角度方向同扇形。驗(yàn)證方法是;驗(yàn)證距離與夾角。
2、扇形邊為軸,圓形半徑為大小組成的膠囊體空間,由于扇形的對(duì)稱性,我們可以通過(guò)把圓心映射到一側(cè),從而只需要計(jì)算1條邊。
定義扇形:
/// <summary>
/// 扇形區(qū)間。
/// </summary>
public struct SectorArea
{
public Vector2 o;
public float r;
public Vector2 direction;
public float angle;
}相交檢測(cè):
/// <summary>
/// 判斷圓形與扇形相交。
/// </summary>
/// <param name="sectorArea"></param>
/// <param name="target"></param>
/// <returns></returns>
public static bool Sector(SectorArea sectorArea, CircleArea target)
{
Vector2 tempDistance = target.o - sectorArea.o;
float halfAngle = Mathf.Deg2Rad * sectorArea.angle / 2;
if (tempDistance.sqrMagnitude < (sectorArea.r + target.r) * (sectorArea.r + target.r))
{
if (Vector3.Angle(tempDistance, sectorArea.direction) < sectorArea.angle / 2)
{
return true;
}
else
{
Vector2 targetInSectorAxis = new Vector2(Vector2.Dot(tempDistance,
sectorArea.direction), Mathf.Abs(Vector2.Dot(tempDistance, new Vector2(-sectorArea.direction.y, sectorArea.direction.x))));
Vector2 directionInSectorAxis = sectorArea.r * new Vector2(Mathf.Cos(halfAngle), Mathf.Sin(halfAngle));
return SegmentPointSqrDistance(Vector2.zero, directionInSectorAxis, targetInSectorAxis) <= target.r * target.r;
}
}
return false;
}圓形與凸多邊形
定義多邊形:
/// <summary>
/// 多邊形區(qū)域。
/// </summary>
public struct PolygonArea
{
public Vector2[] vertexes;
}相交檢測(cè):
/// <summary>
/// 判斷多邊形與圓形相交
/// </summary>
/// <param name="polygonArea"></param>
/// <param name="target"></param>
/// <returns></returns>
public static bool PolygonS(PolygonArea polygonArea, CircleArea target)
{
if (polygonArea.vertexes.Length < 3)
{
Debug.Log("多邊形邊數(shù)小于3.");
return false;
}
#region 定義臨時(shí)變量
//圓心
Vector2 circleCenter = target.o;
//半徑的平方
float sqrR = target.r * target.r;
//多邊形頂點(diǎn)
Vector2[] polygonVertexes = polygonArea.vertexes;
//圓心指向頂點(diǎn)的向量數(shù)組
Vector2[] directionBetweenCenterAndVertexes = new Vector2[polygonArea.vertexes.Length];
//多邊形的邊
Vector2[] polygonEdges = new Vector2[polygonArea.vertexes.Length];
for (int i = 0; i < polygonArea.vertexes.Length; i++)
{
directionBetweenCenterAndVertexes[i] = polygonVertexes[i] - circleCenter;
polygonEdges[i] = polygonVertexes[i] - polygonVertexes[(i + 1)% polygonArea.vertexes.Length];
}
#endregion
#region 以下為圓心處于多邊形內(nèi)的判斷。
//總夾角
float totalAngle = Vector2.SignedAngle(directionBetweenCenterAndVertexes[polygonVertexes.Length - 1], directionBetweenCenterAndVertexes[0]);
for (int i = 0; i < polygonVertexes.Length - 1; i++)
totalAngle += Vector2.SignedAngle(directionBetweenCenterAndVertexes[i], directionBetweenCenterAndVertexes[i + 1]);
if (Mathf.Abs(Mathf.Abs(totalAngle) - 360f) < 0.1f)
return true;
#endregion
#region 以下為多邊形的邊與圓形相交的判斷。
for (int i = 0; i < polygonEdges.Length; i++)
if (SegmentPointSqrDistance(polygonVertexes[i], polygonEdges[i], circleCenter) < sqrR)
return true;
#endregion
return false;
}圓形與AABB
定義AABB:
/// <summary>
/// AABB區(qū)域
/// </summary>
public struct AABBArea
{
public Vector2 center;
public Vector2 extents;
}AABB是凸多邊形的特例,是長(zhǎng)寬邊分別與X/Y軸平行的矩形,這里我們要充分的利用他的對(duì)稱性。
1 利用對(duì)稱性將目標(biāo)圓心映射到,以AABB中心為原點(diǎn)、兩邊為坐標(biāo)軸的坐標(biāo)系,的第一象限
2 將目標(biāo)圓心映射到,以AABB第一象限角點(diǎn)為原點(diǎn)、兩邊為坐標(biāo)軸的坐標(biāo)系,的第一象限
3 最后只需要判斷圓形半徑與步驟2中映射點(diǎn)的向量大小
相交檢測(cè):
/// <summary>
/// 判斷AABB與圓形相交
/// </summary>
/// <param name="aABBArea"></param>
/// <param name="target"></param>
/// <returns></returns>
public static bool AABB(AABBArea aABBArea, CircleArea target)
{
Vector2 v = Vector2.Max(aABBArea.center - target.o, -(aABBArea.center - target.o));
Vector2 u = Vector2.Max(v - aABBArea.extents,Vector2.zero);
return u.sqrMagnitude < target.r * target.r;
}圓形與OBB
定義OBB:
/// <summary>
/// OBB區(qū)域
/// </summary>
public struct OBBArea
{
public Vector2 center;
public Vector2 extents;
public float angle;
}OBB相對(duì)于AABB,矩形邊不與坐標(biāo)軸重合,對(duì)于它和圓形的相交檢測(cè)只需要把圓形旋轉(zhuǎn)到OBB邊所在坐標(biāo)系中,剩下的步驟與AABB的相同。
相交檢測(cè):
/// <summary>
/// 判斷OBB與圓形相交
/// </summary>
/// <param name="oBBArea"></param>
/// <param name="target"></param>
/// <returns></returns>
public static bool OBB(OBBArea oBBArea, CircleArea target)
{
Vector2 p = oBBArea.center - target.o;
p = Quaternion.AngleAxis(-oBBArea.angle, Vector3.forward) * p;
Vector2 v = Vector2.Max(p, -p);
Vector2 u = Vector2.Max(v - oBBArea.extents, Vector2.zero);
return u.sqrMagnitude < target.r * target.r;
}看完這篇關(guān)于Unity如何實(shí)現(xiàn)圖形相交檢測(cè)的文章,如果覺(jué)得文章內(nèi)容寫(xiě)得不錯(cuò)的話,可以把它分享出去給更多人看到。
網(wǎng)頁(yè)名稱:Unity如何實(shí)現(xiàn)圖形相交檢測(cè)
文章網(wǎng)址:http://m.kartarina.com/article40/jeccho.html
成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián),為您提供商城網(wǎng)站、云服務(wù)器、網(wǎng)站制作、App開(kāi)發(fā)、品牌網(wǎng)站建設(shè)、域名注冊(cè)
聲明:本網(wǎng)站發(fā)布的內(nèi)容(圖片、視頻和文字)以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主,如果涉及侵權(quán)請(qǐng)盡快告知,我們將會(huì)在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場(chǎng),如需處理請(qǐng)聯(lián)系客服。電話:028-86922220;郵箱:631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載,或轉(zhuǎn)載時(shí)需注明來(lái)源: 創(chuàng)新互聯(lián)

- 欲知企業(yè)網(wǎng)站制作做得如何,一測(cè)便知 2021-11-22
- 企業(yè)網(wǎng)站制作空間選擇需要注意那些方面 2021-10-09
- 企業(yè)網(wǎng)站制作該如何報(bào)價(jià) 2021-11-25
- 企業(yè)網(wǎng)站制作哪些欄目是必須要有的 2015-03-30
- 深圳網(wǎng)站建設(shè)哪家好,創(chuàng)新互聯(lián)介紹企業(yè)網(wǎng)站制作可選用的三種方法 2014-12-13
- 成都企業(yè)網(wǎng)站制作需要多長(zhǎng)時(shí)間_成都網(wǎng)站建設(shè)創(chuàng)新互聯(lián)科技 2021-11-16
- 企業(yè)網(wǎng)站制作完后如何做網(wǎng)站優(yōu)化推廣 2017-05-06
- 企業(yè)網(wǎng)站制作行業(yè)風(fēng)險(xiǎn)控制 2021-08-13
- 選擇專業(yè)靠譜的成都企業(yè)網(wǎng)站制作公司 2023-02-21
- 企業(yè)網(wǎng)站制作如何分析對(duì)手網(wǎng)站 2021-11-17
- 成都企業(yè)網(wǎng)站制作內(nèi)容構(gòu)成包括哪些 2016-08-23
- 成都企業(yè)網(wǎng)站制作要注意哪些問(wèn)題 2022-12-30