C語言中二叉樹的常見操作是什么-創(chuàng)新互聯(lián)

這篇文章主要講解了“C語言中二叉樹的常見操作是什么”，文中的講解內(nèi)容簡單清晰，易于學(xué)習(xí)與理解，下面請大家跟著小編的思路慢慢深入，一起來研究和學(xué)習(xí)“C語言中二叉樹的常見操作是什么”吧！

創(chuàng)新互聯(lián)公司是一家專業(yè)提供霍林郭勒企業(yè)網(wǎng)站建設(shè),專注與做網(wǎng)站、網(wǎng)站設(shè)計、html5、小程序制作等業(yè)務(wù)。10年已為霍林郭勒眾多企業(yè)、政府機(jī)構(gòu)等服務(wù)。創(chuàng)新互聯(lián)專業(yè)的建站公司優(yōu)惠進(jìn)行中。

一、基本概念

每個結(jié)點(diǎn)最多有兩棵子樹，左子樹和右子樹，次序不可以顛倒。

性質(zhì)：

1、非空二叉樹的第n層上至多有2^(n-1)個元素。

2、深度為h的二叉樹至多有2^h-1個結(jié)點(diǎn)。

滿二叉樹：所有終端都在同一層次，且非終端結(jié)點(diǎn)的度數(shù)為2。

在滿二叉樹中若其深度為h，則其所包含的結(jié)點(diǎn)數(shù)必為2^h-1。

完全二叉樹：除了較大的層次即成為一顆滿二叉樹且層次較大那層所有的結(jié)點(diǎn)均向左靠齊，即集中在左面的位置上，不能有空位置。

對于完全二叉樹，設(shè)一個結(jié)點(diǎn)為i則其父節(jié)點(diǎn)為i/2，2i為左子節(jié)點(diǎn)，2i+1為右子節(jié)點(diǎn)。

二、存儲結(jié)構(gòu)

順序存儲：

將數(shù)據(jù)結(jié)構(gòu)存在一塊固定的數(shù)組中。

#define LENGTH 100
typedef char datatype;
typedef struct node{
  datatype data;
  int lchild,rchild;
  int parent;
}Node;
Node tree[LENGTH];
int length;
int root;

雖然在遍歷速度上有一定的優(yōu)勢，但因所占空間比較大，是非主流二叉樹。二叉樹通常以鏈?zhǔn)酱鎯Α?/p>

鏈?zhǔn)酱鎯Γ?/strong>

typedef char datatype;
typedef struct BinNode{
  datatype data;
  struct BinNode* lchild;
  struct BinNode* rchild;
}BinNode;
typedef BinNode* bintree;     //bintree本身是個指向結(jié)點(diǎn)的指針

三、二叉樹的遍歷

遍歷即將樹的所有結(jié)點(diǎn)訪問且僅訪問一次。按照根節(jié)點(diǎn)位置的不同分為前序遍歷，中序遍歷，后序遍歷。

前序遍歷：根節(jié)點(diǎn)->左子樹->右子樹

中序遍歷：左子樹->根節(jié)點(diǎn)->右子樹

后序遍歷：左子樹->右子樹->根節(jié)點(diǎn)

例如：求下面樹的三種遍歷

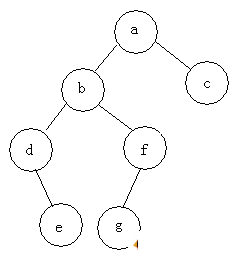
前序遍歷：abdefgc

中序遍歷：debgfac

后序遍歷：edgfbca

四、遍歷的實現(xiàn)

遞歸實現(xiàn)(以前序遍歷為例，其他的只是輸出的位置稍有不同)

void preorder(bintree t){
  if(t){
    printf("%c ",t->data);
    preorder(t->lchild);
    preorder(t->rchild);
  }
}

非遞歸的實現(xiàn)

因為當(dāng)遍歷過根節(jié)點(diǎn)之后還要回來，所以必須將其存起來。考慮到后進(jìn)先出的特點(diǎn)，選用棧存儲。數(shù)量確定，以順序棧存儲。

#define SIZE 100
typedef struct seqstack{
  bintree data[SIZE];
  int tag[SIZE];  //為后續(xù)遍歷準(zhǔn)備的
  int top;   //top為數(shù)組的下標(biāo)
}seqstack;
void push(seqstack *s,bintree t){
  if(s->top == SIZE){
    printf("the stack is full\n");
  }else{
    s->top++;
    s->data[s->top]=t;
  }
}
bintree pop(seqstack *s){
  if(s->top == -1){
    return NULL;
  }else{
    s->top--;
    return s->data[s->top+1];
  }
}

1、前序遍歷

void preorder_dev(bintree t){
  seqstack s;
  s.top = -1;   //因為top在這里表示了數(shù)組中的位置，所以空為-1
  if(!t){
    printf("the tree is empty\n");
  }else{
    while(t || s.stop != -1){
      while(t){  //只要結(jié)點(diǎn)不為空就應(yīng)該入棧保存，與其左右結(jié)點(diǎn)無關(guān)
         printf("%c ",t->data);
        push(&s,t);
        t= t->lchild;
      }
      t=pop(&s);
      t=t->rchild;
    }
  }
}

2、中序遍歷

void midorder(bintree t){
  seqstack s;
  s.top = -1;
  if(!t){
    printf("the tree is empty!\n");
  }else{
    while(t ||s.top != -1){
      while(t){
        push(&s,t);
        t= t->lchild;
      }
      t=pop(&s);
      printf("%c ",t->data);
      t=t->rchild;
    }
  }
}

3、后序遍歷

因為后序遍歷最后還要要訪問根結(jié)點(diǎn)一次，所以要訪問根結(jié)點(diǎn)兩次。采取夾標(biāo)志位的方法解決這個問題。

這段代碼非常糾結(jié)，對自己有信心的朋友可以嘗試獨(dú)立寫一下。反正我是寫了很長時間。邏輯不難，我畫了一張邏輯圖：

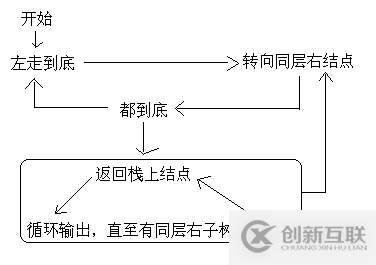
代碼：

void postorder_dev(bintree t){
  seqstack s;
  s.top = -1;
  if(!t){
    printf("the tree is empty!\n");
  }else{
    while(t || s.top != -1){  //棧空了的同時t也為空。
      while(t){
        push(&s,t);
        s.tag[s.top] = 0;  //設(shè)置訪問標(biāo)記，0為第一次訪問，1為第二次訪問
        t= t->lchild;
      }
      if(s.tag[s.top] == 0){ //第一次訪問時，轉(zhuǎn)向同層右結(jié)點(diǎn)
        t= s.data[s.top];  //左走到底時t是為空的，必須有這步！
        s.tag[s.top]=1;
        t=t->rchild;
      }else {
        while (s.tag[s.top] == 1){ //找到棧中下一個第一次訪問的結(jié)點(diǎn)，退出循環(huán)時并沒有pop所以為其左子結(jié)點(diǎn)
          t = pop(&s);
          printf("%c ",t->data);
        }
        t = NULL; //必須將t置空。跳過向左走，直接向右走
      }
    }
  }
}

4、層次遍歷：即每一層從左向右輸出

元素需要儲存有先進(jìn)先出的特性，所以選用隊列存儲。

隊列的定義：

#define MAX 1000
typedef struct seqqueue{
  bintree data[MAX];
  int front;
  int rear;
}seqqueue;
void enter(seqqueue *q,bintree t){
  if(q->rear == MAX){
    printf("the queue is full!\n");
  }else{
    q->data[q->rear] = t;
    q->rear++;
  }
}
bintree del(seqqueue *q){
  if(q->front == q->rear){
    return NULL;
  }else{
    q->front++;
    return q->data[q->front-1];
  }
}

遍歷實現(xiàn)

void level_tree(bintree t){
  seqqueue q;
  bintree temp;
  q.front = q.rear = 0;
  if(!t){
    printf("the tree is empty\n");
    return ;
  }
  enter(&q,t);
  while(q.front != q.rear){
    t=del(&q);
    printf("%c ",t->data);
    if(t->lchild){
      enter(&q,t->lchild);
    }
    if(t->rchild){
      enter(&q,t->rchild);
    }
  }
}

5、利用前序遍歷的結(jié)果生成二叉樹

//遞歸調(diào)用，不存點(diǎn)，想的時候只關(guān)注于一個點(diǎn)，因為還會回來的，不要跟蹤程序運(yùn)行，否則容易多加循環(huán)
void createtree(bintree *t){
  datatype c;
  if((c=getchar()) == '#')
    *t = NULL;
  else{
    *t = (bintree)malloc(sizeof(BinNode));
    (*t)->data = c;
    createtree(&(*t)->lchild);
    createtree(&(*t)->rchild);
  }
}

6、二叉樹的查找

bintree search_tree(bintree t,datatype x){
  if(!t){
    return NULL;
  }
  if(t->data == x){
    return t;
  }else{
    if(!search_tree(t->lchild,x)){
      return search_tree(t->rchild,x);
    }
    return t;
  }
}

7、統(tǒng)計結(jié)點(diǎn)個數(shù)

int count_tree(bintree t){
  if(t){
    return (count_tree(t->lchild)+count_tree(t->rchild)+1);
  }
  return 0;
}

8、比較兩個樹是否相同

int is_equal(bintree t1,bintree t2){
  if(!t1 && !t2){   //都為空就相等
    return 1;
  }
  if(t1 && t2 && t1->data == t2->data){   //有一個為空或數(shù)據(jù)不同就不判斷了
    if(is_equal(t1->lchild,t2->lchild))
      if(is_equal(t1->rchild,t2->rchild)){
        return 1;
      }
  }
  return 0;
}

9、求二叉樹的深度

int hight_tree(bintree t){
  int h,left,right;
  if(!t){
    return 0;
  }
  left = hight_tree(t->lchild);
  right = hight_tree(t->rchild);
  h = (left>right?left:right)+1;
  return h;
}

感謝各位的閱讀，以上就是“C語言中二叉樹的常見操作是什么”的內(nèi)容了，經(jīng)過本文的學(xué)習(xí)后，相信大家對C語言中二叉樹的常見操作是什么這一問題有了更深刻的體會，具體使用情況還需要大家實踐驗證。這里是創(chuàng)新互聯(lián)網(wǎng)站建設(shè)公司，，小編將為大家推送更多相關(guān)知識點(diǎn)的文章，歡迎關(guān)注！

網(wǎng)站名稱：C語言中二叉樹的常見操作是什么-創(chuàng)新互聯(lián)
URL標(biāo)題：http://m.kartarina.com/article12/ccgigc.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供營銷型網(wǎng)站建設(shè)、網(wǎng)站營銷、商城網(wǎng)站、域名注冊、云服務(wù)器、定制開發(fā)

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會在第一時間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時需注明來源： 創(chuàng)新互聯(lián)